End Behavior Of A Function

End Beliefs of a Function

The end beliefs of a polynomial function is the beliefs of the graph of $f (ten)$ equally $x$ approaches positive infinity or negative infinity.

The degree and the leading coefficient of a polynomial part make up one's mind the end beliefs of the graph.

The leading coefficient is significant compared to the other coefficients in the function for the very large or very small numbers. So, the sign of the leading coefficient is sufficient to predict the finish behavior of the function.

Degree	Leading Coefficient	End behavior of the function	Graph of the function
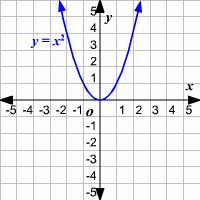
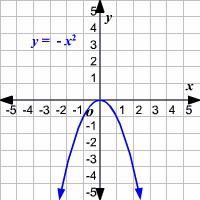
Even	Positive	$\begin{array}{l} f (x) \to + \infty, as x \to - \infty \\ f (x) \to + \infty, as 10 \to + \infty \end{array}$	Example: $f (x) = x^{2}$
Even	Negative	$\begin{array}{l} f (x) \to - \infty, every bit x \to - \infty \\ f (x) \to - \infty, equally x \to + \infty \end{array}$	Example: $f (10) = - x^{2}$
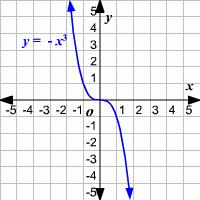
Odd	Positive	$\begin{array}{l} f (ten) \to - \infty, as x \to - \infty \\ f (x) \to + \infty, as x \to + \infty \end{array}$	Example: $f (10) = {ten}^{3}$
Odd	Negative	$\begin{array}{l} f (x) \to + \infty, as x \to - \infty \\ f (10) \to - \infty, as 10 \to + \infty \end{array}$	Instance: $f (x) = - 10^{3}$

To predict the cease-beliefs of a polynomial function, first check whether the function is odd-degree or even-degree role and whether the leading coefficient is positive or negative.

Example:

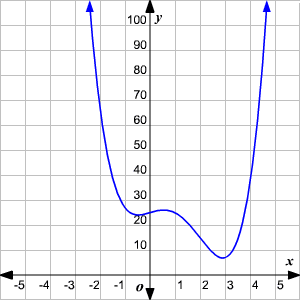
Discover the end behavior of the role $x^{4} - 4 x^{three} + 310 + 25$ .